Research topics
- Microorganism locomotion and cellular mechanics
- Suspensions of interacting and active particles
- Mechanics of soft materials and complex fluids
- Low Reynolds number hydrodynamics
- Numerical methods and computational mathematics
Research description
Broadly speaking, my research interests lie in the development and usage of
computational techniques to study the dynamics of microscopic objects in fluid.
These objects can interact with each other through a variety of interparticle
forces allowing them to self-assemble to form structures, they can be
sufficiently small that they move stochastically through the fluid due to thermal
fluctuations, they can be deformable, allowing for shape changes in reponse
to applied forces, or they can have an interesting shape that allows them to move
through the surrounding fluid in peculiar ways. I have particular interest when these objects
are biological, especially swimming cells and microorganisms that can generate
fluid flows as they move through their surrounding environment.
The computational techniques I develop address the problem of simulating the dynamics of these objects both at the individual level using highly resolved schemes, as well as at the large-scale (up to hundreds of thousands in some cases) to study how their coupled motion may lead to collective dynamics.
Possible PhD projects Please note that these descriptions are here to start a conversation and give a flavour of the kind of projects that you could be working on. If you have questions about certain projects and your suitability for them, please do get in touch.
- Mechanics of cilia coordination: Cells often use slender, elastic structures to generate fluid motion. A prime example is the cilia in our lungs that facilitate mucus transport. Interactions between the cilia can give rise to their coordinated motion, which in turn produces fluid motion at a much larger scale. Using computational models that we have recently developed, the project will include exploring the mechanics of this coupling and determining the underlying mechanisms that give rise to different coordinated states. Familiarity with fluid mechanics, especially at low Reynolds number, numerical methods of differential equations, computational linear algebra, and strong programming skills will be useful.
- Interacting particles in viscoelastic fluids: Many biological fluids, as well as those arising in industrial processes, are viscoelastic due to the presence of polymers suspended in the liquid. The project will entail developing techiques for large-scale simulation that resolve the motion and interactions of either rigid or deformable bodies suspended in these fluids. The project will require a background in fluid mechanics and transport processes, as well as in numerical methods for PDEs. Strong programming skills are also highly desirable.
- Stochastic simulation of Brownian particles: Including the effects of Brownian motion in suspension simulations has traditionally been a computationally intensive endeavour. Only recently in the past 5-10 years have Brownian computations have been accelerated by using ideas from fluctuating hydrodynamics. The project builds on this work and aims at extending these ideas to new scenarios and problems in this burgeoning research area. This project requires a background in fluid mechanics and/or statistical mechanics, applied stochastic processes, and numerical methods for ODEs and SDEs.
- Dynamics and interactions of shape-changing particles: While many tiny objects, such as microorganisms, change their shape with time, the models we use to understand their interactions are based on rigid particles. This project entails developing models for their interactions that account for the shape change and the timescale over which they occur. The project requires a background in fluid mechanics, especially at low Reynolds number, asymptotic methods, and a background in numerical methods for PDEs.
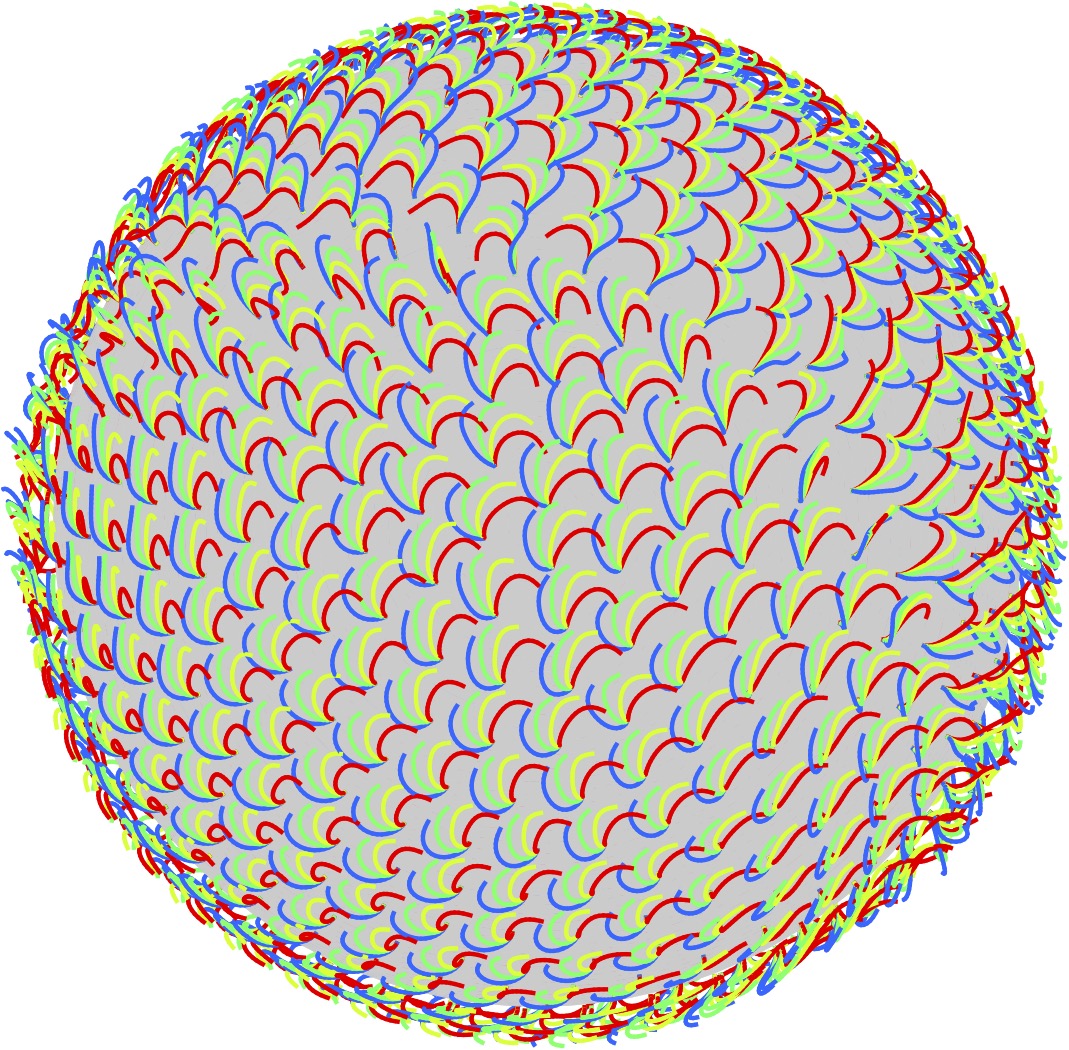
The coordinated movement of active filaments on a sphere from Westwood and Keaveny 2021

Simulation of a suspension of sperm cells from Schoeller and Keaveny 2018

Snapshot of a simulation containing 40K model swimming microorganisms from Delmotte et al. 2015
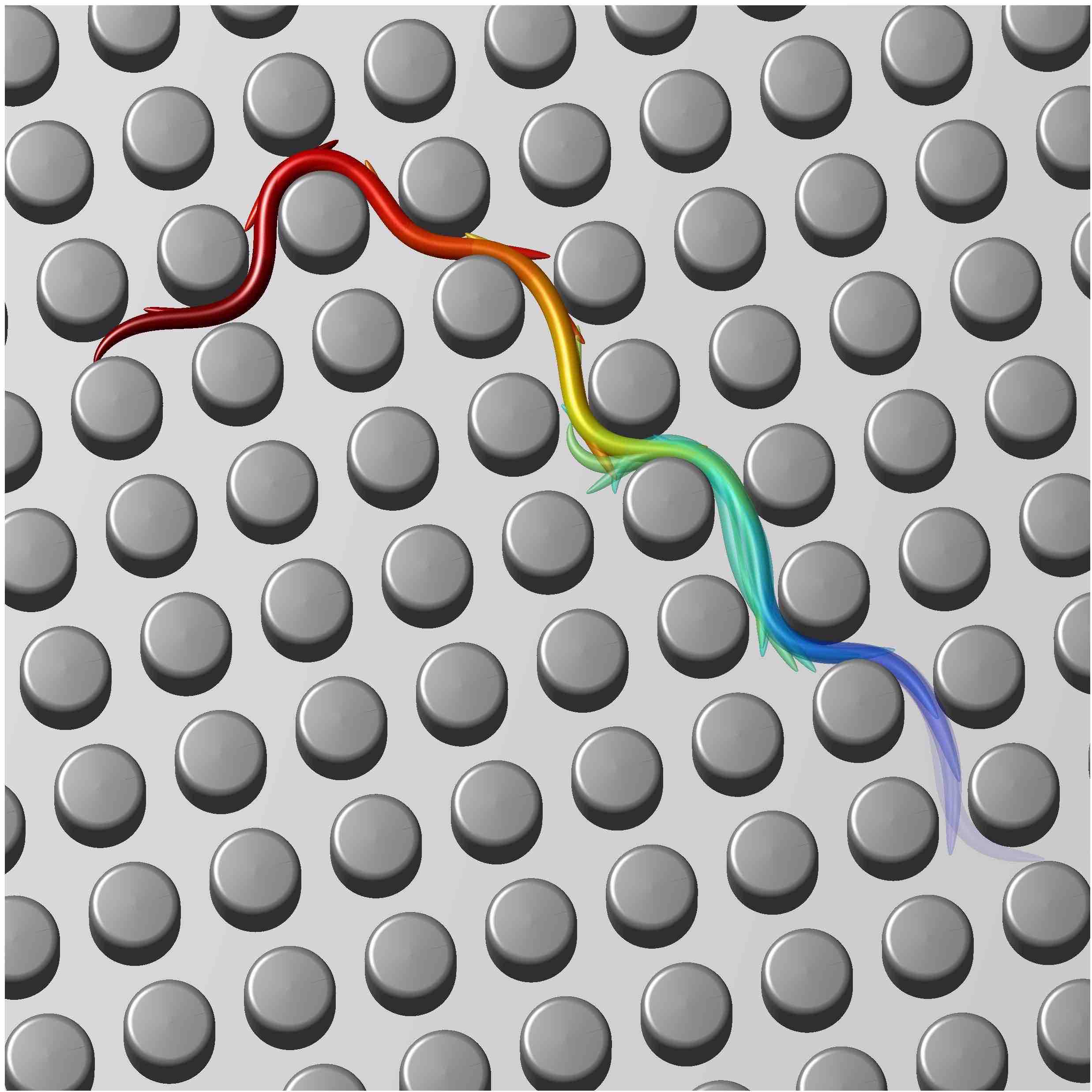
Simulation of C. elegans moving through a structured environment from Majmudar et al. 2012